Research Location
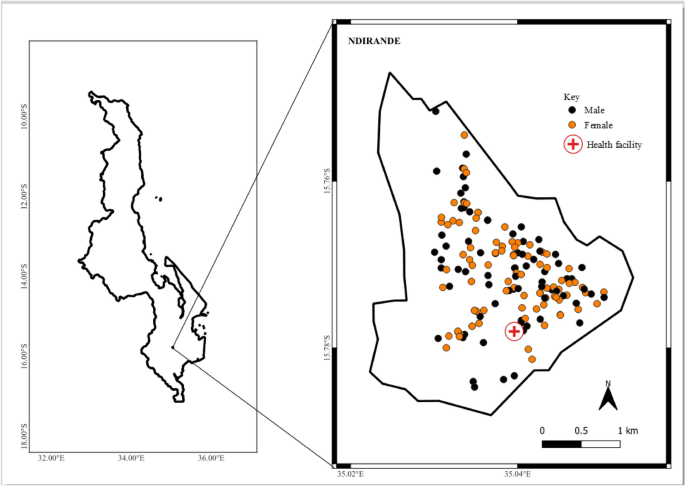
The study was conducted from October 2016 to February 2020 in Ndilande District, Blantyre, Malawi. The district had a population of approximately 100,000 in 2018, an area of approximately 6.7 km2, and is home to one government clinic6. Blantyre is located in southern Malawi, east of the Greenwich Meridian and south of the Equator. Blantyre was chosen for the study because it is well known for its high burden of typhoid fever and has the research capacity to conduct complex studies6.
Malawi has two main climatic seasons: rainy and dry. The rainy season is further divided into early rainy (November-February) and late rainy (March-April) seasons. 7 Similarly, the dry season is divided into cool dry (May-August) and hot dry (September-October) seasons. 7 A recent study protocol reported that the monthly number of typhoid cases in Ndirande Township, Blantyre District, Malawi, increased during Malawi’s rainy season from December to February. 6 Ndirande’s elevation ranges from 970 meters to 1200 meters, with an average elevation of 1118 meters. Total precipitation also varied from 819 millimeters (mm) to 1602 mm from 2016 to 2019. However, the variation in total precipitation across Ndirande was minimal, with a maximum difference of 209 mm from year to year. In this study, season was included in the modelling as a temporal covariate.
data
STRAATA Project Passive Monitoring Research
The Strategic Typhoid Alliance in Africa and Asia (STRATAA) study was conducted in three countries, Bangladesh, Nepal and Malawi, with the aim of measuring the burden of typhoid in these three countries. 6 In Malawi, the STRATAA study was conducted by the Malawi Wellcome Liverpool Clinical Research Programme in the largest government-run clinic in Ndilande Township. This paper focuses on the passive surveillance sub-study of the STRATAA project.
In the passive surveillance study, patients who presented to Ndirande clinic with a history of fever for at least 2 days or a temperature of at least 38.0°C were approached to consider enrolling in the study. Passive surveillance was further conducted at Queen Elizabeth Central Hospital (QECH) for patients from Ndirande who presented to the Acute Care Centre (AETC) or were admitted to the ward. Blood cultures were taken from patients who consented to enroll in the study. A total of 161 typhoid cases were recorded at Ndirande clinic between October 2016 and February 2020 in the passive surveillance study. The sex and age of study participants were collected as part of the routine data collected in the study; however, one case did not have a collection date and was therefore excluded from the analysis. The household location (latitude and longitude) of typhoid cases was collected using a portable Global Positioning System (GPS) device.
Our models included two indicators: sex (male or female) of typhoid cases and age. Age was categorized into three levels (0–5 years, 6–17 years, and ≥18 years) based on previous studies of the association between typhoid fever and several age groups.
Population Data
The STRATAA study also conducted a household- and individual-level census in 2018. The census, which counted 102,242 people, was used as an offset in the model.
Spatial covariates
The selection of covariates was based on previous studies on the association between typhoid fever and environmental covariates. In this study, we focused on covariates available at a spatial resolution of 100 m2 in Ndirande. Thus, the spatial covariates are distance to health clinic (meters), altitude (meters), and water, sanitation, and hygiene (WASH) score in Ndirande.
The distance to clinic raster was obtained by calculating the Euclidean distance from each location in Ndirande County to the clinic. The elevation raster file was downloaded from the WorldPop website. The raster was cropped to a 100 m2 Ndirande grid.
In 2018, a water, sanitation and hygiene (WASH) survey was conducted among 14,136 households in Ndilande County as part of the STRATAA study. WASH variables were self-reported in the questionnaire. WASH scores were calculated using principal component analysis (PCA) and linear geostatistical models were used to interpolate WASH scores on a grid. Further details on spatial covariates, including how WASH scores were calculated, are provided in the Supplementary Material.
Modeling typhoid cases using point pattern models
We developed a non-homogeneous spatial marked point process model that can incorporate both spatial and individual-level covariates as marks25. Let i represent the subscript for gender, where \(i=1\) corresponds to “male” and \(i=2\) corresponds to “female”. We then use j to represent the subscript that identifies a particular age group, where \(j=1\) represents individuals aged 0-5 years, \(j=2\) represents individuals aged 6-17 years, and \(j=3\) represents individuals aged 17 years or older. The outcome variable corresponds to the location of the reported diagnosed case x contained in A, which represents the area bounded by the boundaries of Ndirande County. Thus, \(n_{ij}\) corresponds to the number of typhoid cases in a particular age-gender combination. By setting age and gender as marks, we model the reported cases within each age-gender subgroup as an independent non-homogeneous Poisson process. Specifically, we model the subgroup strength of gender i and age j as \(\lambda _{ij}\left( {x}\right) = \exp \left( \alpha _{i} + \gamma _{j} + d\left( {x} \right) ^{\prime }\beta + \log {m_{ij}(x)} \right).\). In the strength equation, we use \(\alpha _{i}\) to account for the effect of gender and \(\gamma _{j}\) to account for differences between age groups. The vector \(d\left( {x} \right)\) represents a linear combination of spatial covariates. The spatial covariates are distance to Ndirande health clinic (in meters) (\(\beta _1\)), altitude (in meters) (\(\beta _2\)), and WASH score (\(\beta _3\)). Finally, \({m_{ij}(x)}\) is the offset corresponding to the population of individuals of gender i and age j at location x.
We denote the vector of unknown parameters by \(\theta\), which consists of the intercept and regression coefficients \(\beta\) that quantify the effect of gender (\(\alpha _i\), for \(i=1,2\)) and age (\(\gamma _j\), for \(j=1,2,3\)). The likelihood function for \(\theta\) is expressed as:
$$\begin{aligned} L(\theta ) = \sum _{i=1}^{2} \sum _{j=1}^{3} L_{ij}(\theta ) \end{aligned} $$
(1)
where
$$\begin{aligned} L_{ij}(\theta )=\sum _{k=1}^{n_{ij}} \log \lambda _{ij} \left( {x}_{k} \ right) – \int _{A} \lambda _{ij}\left( {x} \right) d {x} \end{aligned}$$
(2)
We approximate the integral in (2) using quadrature based on a 100 m × 100 m regular grid of the study area shown in A26. To obtain confidence intervals for the parameter \(\theta\), we use a parametric bootstrap27 based on the following iterative steps:
1.
Simulate N = 10,000 samples from the mean-fitted point process model.
$$\begin{aligned} \lambda _{ij}\left( {x}\right) = \exp \left( \alpha _{i} + \gamma _{j} + d\left( {x} \ right) ^{\prime }\beta + \log {m_{ij}(x)} \right) \end{aligned}$$
(3)
2.
Fit the model to the N bootstrap realizations simulated in step (1).
3.
Save the parameter estimates from each fitted model.
Four.
Use the percentile method to obtain 95% confidence intervals from the estimates stored in step (3).
We fitted both the spatial model (2) and the spatiotemporal model (Equation 3 in the Supporting Information) to the data. Under the null hypothesis that the data should be fitted using a spatial model, we tested for temporal trends in the data by comparing a purely spatial model with a model with temporal covariates using a likelihood ratio test.
We calculated the predicted incidence for each combination of marks (age and sex) while adjusting for spatial covariates and population as defined by the intensity equation above: \(\left( \lambda _{ij}\left( {x}\right) = \exp \left( \alpha _{i} + \gamma _{j} + d\left( {x} \right) ^{\prime }\beta + \log {m_{ij}(x)} \right) \right)\). In addition to plotting the predicted incidence by age and sex on a regular 100m × 100m grid, we also estimated incidence for the entire area of Ndirande, defined as:
$$\begin{aligned} \frac{\int _{A} \lambda _{ij}(x) dx}{ \int _{A} m_{ij} (x) dx}. \end{aligned}$ $
(Four)
The integral in Equation 4 was approximated using a regular grid with a spatial resolution of 100m × 100m.
Validating the model
To verify the fit of the spatial point pattern model presented in the previous section to the data, we develop a simulation procedure based on the K-function, which is expressed as follows28.
$$\begin{aligned} {\widehat{K}}(r)=\frac{1}{D|W|} \sum _{h} \sum _{k \ne h} \frac{I\left \{ || x_{k}-x_{h}|| \le r\right\} }{\hat{\lambda }\left( x_{k}\right) \hat{\lambda }\left( x_ {h}\right) }. \end{aligned}$$
(5)
where \(D=\frac{1}{|W|} {\sum }_{h} 1/\hat{\lambda }\left( x_{h}\right)\); r is the distance at which the function is evaluated. \(\hat{\lambda }(x)\) is the estimated intensity from the model at location x. \(I\left\{ || x_{k}-x_{h}||\right\}\) is an indicator function that takes the value 1 if the absolute distance between any two locations \(x_{k}\) and \(x_{h}\) is less than or equal to r, and 0 otherwise.
We then validate the model using the following bootstrap procedure:
1.
Entering a maximum likelihood estimate of \(\theta\), we can simulate a data set based on the heterogeneous marked point process defined in the previous section.
2.
For the dataset simulated in the previous step, we compute the non-homogeneous K-function defined in (5).
3.
Repeat (1) and (2) 10,000 times.
Four.
For a defined set of distances, calculate a 95\(\%\) confidence interval using the 10,000 functions obtained in the previous step.
Once the final step is complete, if the K-function calculated on the original data falls within the 95\(\%\) envelope for each age-gender combination, it is concluded that the data show no evidence against the fitted model.
Ethical considerations
The Oxford Tropical Research Ethics Committee (reference number 39-15) and the Malawi National Health Sciences Research Council (reference number 15/5/1599) approved the STRATAA study (trial number ISRCTN 12131979) to be conducted in Malawi. At the household level, the head of the household provided written informed consent for the household survey on behalf of the entire household. In other components of the STRATAA study, study participants aged 18 years or older signed informed consent forms. Meanwhile, parents or guardians of children under 18 years signed informed consent forms. In addition, consent was sought from children aged 11 to 17 years. We confirm that the methods carried out in this study were carried out in accordance with the appropriate regulations and guidelines. Furthermore, we confirm that this study complies with the Declaration of Helsinki.